如何搭建一个 full-text search 引擎

在文档中查询的技术

Posted on 2020/7/11

Contents

当我们使用搜索引擎，使用网站或者在线服务内置的搜索功能，或者管理本地的文本文件的时候，都会面临这样一种需求：如何在大量的自然语言文本中快速找到符合特定模式的部分？对于精确的字符串匹配，当然已经有成熟的算法了。但是更多的时候我们需要处理更复杂的需求：用户可能只记得大概的模式，因此我们的搜索功能应该能够在一定限度内容忍不一致；为了让用户能够更快找到有用的信息，我们需要将搜索的结果按照 “相关性” 排序；为了让交互更加直观，我们需要向用户展示一些预览文本，从而让用户能够了解自己搜索到了什么。

下图展示了搜索引擎的一个用例，我们可以从中看到上面这些机制的运作。当我们搜索 post punk bands 1980s 时，它不会严格地匹配这个字符串，而是能够容忍一些改动，例如将 post 和 punk 之间用连字符连接，或者把 1980s 替换成 1980。尽管可以容忍一些关键词的缺失，但是它仍然能够衡量某个网页和查询的相关程度，例如 List of post punk-bands 的 wiki 就比 post-punk 的 wiki 排名靠前。

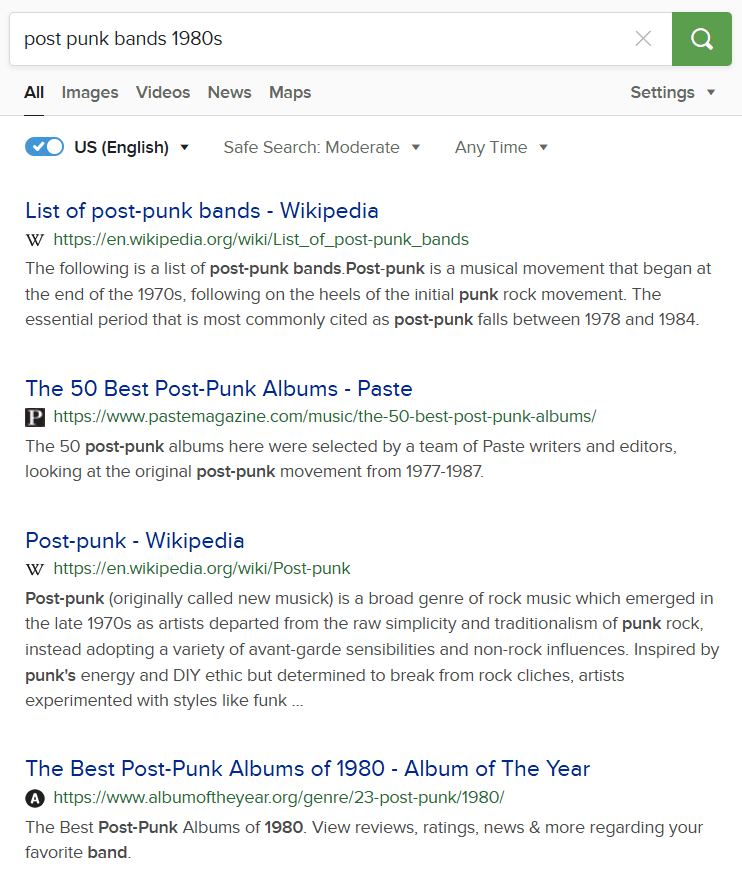
催生本文的是这样一个场景：某日看到我在我的 Telegram channel 写下的几百条文字，但是又想到 Telegram 的聊天记录搜索对于中文相当不友好（详情可以参考这篇文章），如果不做一个更好的搜索工具的话，之前写下的文字很快就会淹没在时间线之中，难以被挖掘出来了。于是我便萌生了搭建一个搜索服务的想法，在 GitHub 上稍加搜索就能找到一个叫 telegram-search 的仓库，提供了一个利用 bot 进行搜索的程序。但是当我搭建起来之后，发现了一个问题：这个程序是利用 Elasticsearch 提供搜索服务的，但是我手头的机器内存太小了，无法满足 Elasticsearch 的内存需求，只能使用大量的 swap，这导致搜索过程的稳定性很差。一番考虑之后，决定另寻他法。在一番查找之后，发现了一个纯 python 的库 whoosh 能够提供类似的需求，于是将 telegram-search 的代码一番魔改，做成了 tg-searcher 这个新的服务，占用内存远比 Elasticsearch 小，并且能够达到类似的效果。

在搜索相关内容和写代码的过程中，也顺便了解了一些这些文字搜索库的基本原理。从术语上讲，这种对自然语言文本进行检索的过程被称为全文检索（Full-text search）。本文旨在介绍一个基本的全文检索工具的算法原理和运作的 pipeline，在此基础上可以实现一个全文检索引擎的内核。本文并不会涉及如何进行多线程 / 分布式 / 存储优化 / 性能调优；同时由于本文以介绍原理为主，因此不会涉及一些过于工程化的细节，例如如何设计一个序列化协议。

本文的主要 Reference 是诸全文检索库的文档和源码，以及少量信息检索（Information Retrieval, IR）方面的论文。主要参考的库有一下几个：

whoosh，一个纯 python 的全文检索库，轻量级，文档和代码非常友好
Lucene，一个基于 Java 的全文检索库，历史悠久，文档古色古香
Elasticsearch，基于 Lucene 的一个 Java 库，功能齐全，结构庞大，为分布式架构优化，提供 RESTful 接口
Terrier，同样是基于 Java 的库，（宣称）性能优异，扩展性强，内置了许多算法

这里声明一下本文所用到的一些术语的含义：

查询（query）：用户在进行搜索的时候输入的字符串
关键词（term）：查询中所包含的词语。注：本文中所指的 “关键词” 指的是 term 而不是 keyword，后者一般指的是某一个文档中具有概括性作用的词语
文档（document）：进行查询的对象，通常是由自然语言组成的具有一定长度的字符串
词典（dictionary）：所有关键词组成的集合
文档库（corpus）：所有文档组成的集合

#分词和索引

一个朴素的想法是在进行每次检索时，扫描一遍所有的文档。但是这样做的时间复杂度太高了，尤其是对于大性互联网服务来说，数以亿计的文字，每次都进行搜索无疑是非常低效的。

于是一个所谓的 “倒排索引” （reverse index）就成为一个基本解决方案，它起到了以空间复杂度换时间复杂度的效果。倒排索引的原理很简单：对于每一个词，我们记录它在哪篇文档的哪个位置出现。当我们进行查询的时候，我们将查询的内容分成若干个关键词（term），然后对于每个关键词，我们就可以根据倒排索引查找到这个词在那些文档的那些位置出现，然后将所有这些位置和附近的文本返回个查询者即可。

但是在实现倒排索引之前还有一个问题：我们需要将文字划分成词语。对于英文这一点是比较好解决的，但是对于像中文这样的文字，这个问题就不太 trivial 了。Telegram 的中文搜索体验不佳的主要原因就是它没有对中文进行恰当的分词。如果直接将每个汉字划分成一个词语的话，可能会引发一些歧义。对于中文我们可以使用 jieba 库来进行分词，从下例（来自官方文档）可以看出，它的分词效果还是比较理想的。

from jieba import tokenize
test_str = '工信处女干事每月经过下属科室都要亲口交代24口交换机等技术性器件的安装工作'
for token in tokenize(test_str):
	print(token[0], end=' ')  # token[1] 和 token[2] 分别表示某个词的开始和结束位置
# 输出如下：    
# 工信处 女干事 每月 经过 下属 科室 都 要 亲口 交代 24 口 交换机 等 技术性 器件 的 安装 工作

对于英文来说，虽然不需要进行这样的分词，但是一些预处理也是有必要的，例如将所有字母都换成小写，或者去掉一些没有实际含义的词（称为 stop word，例如 a, with, of 等）。有的时候还需要把所有的词都变成词根，例如把 work, working, worked 都替换成 work（做这项工作的一般被称为 Stemmer）。

这些过程从本质上来说都是把一个字符串转化成一组 token 的序列，人们将实现它的模块称为 analyzer。我们使用 jieba 库中的 tokenizer，建立起倒挂索引，就可以制作出下面这个最简单的中文全文检索工具：

from typing import Dict, Set  # 类型标注
import jieba
from pathlib import Path  # 使用 pathlib 库来进行方便的路径操作
from collections import namedtuple

DocumentPos = namedtuple('DocumentPos', ['document_id', 'start', 'end'])


class Searcher:
    def __init__(self):
        self.reverse_index: Dict[str, Set[DocumentPos]] = {}
        self._document_storage: Dict[int, str] = {}

    def index(self, document: str, uid: int):  
        # 将 document 添加到索引中（uid 是文档的编号）
        document = document.replace('\n', ' ')
        for seg in jieba.tokenize(document, mode='search'):
            word = seg[0]
            document_pos = DocumentPos(uid, seg[1], seg[2])
            if word in self.reverse_index:
                self.reverse_index[word].add(document_pos)
            else:
                self.reverse_index[word] = {document_pos}
        self._document_storage[uid] = document

    def search(self, seg: str) -> Set[DocumentPos]:
        return self.reverse_index.get(seg, {})

    def get_doc_part(self, pos: DocumentPos, padding: int):
        uid, start, end = pos
        return self._document_storage[uid][start - padding: end + padding]
    
if __name__ == '__main__':
    idx = Searcher()
    corpus_path = Path('corpus')  # 存放文档的目录
    for uid, document_path in enumerate(corpus_path.iterdir()):
        idx.index(document_path.read_text(), uid)
    results = idx.search('亲自部署')
    for result in results:
        print(idx.get_doc_part(result, 5))

当文档数量太多的时候，建立起倒排索引需要大量的空间，因此需要将这些索引放在硬盘上持久化，并且通过适当的方式来快速从硬盘中获得需要的索引。持久化的过程、以及如何从硬盘上高效地读取索引常常是全文搜索库的核心，但是由于这不是本文的重点，这里就不多做介绍了；相关信息可以参考 Elasticsearch 或者 Lucene 的文档。

#相关性评估

在找到关键词在文档中出现的位置之后，我们就需要衡量哪篇文档和查询的相关度最高了。当然，我们还是可以想到一个朴素的做法：关键词在哪篇文档中出现的次数之和多，我们就认为哪篇文档的相关度更高。这样的做法有几个问题：

长文档由于包含更多的词语，因此也倾向于包含更多的关键词，因此这样的算法对于短文档 “不公平”。
不同词语的出现频度不同，在进行搜索的时候，比较少间的词（例如 punk）比常用词（例如 how）包含更多的信息量。因此不应当将它们同等看待。

为了解决这些问题，自然我们需要考虑如何进行 “加权”，对较短的文章、较罕见的关键词施加更高的权重。

#tf-idf

一个非常常用的策略被称为 $\text{tf-idf}$ ，它的原理如下：我们用 $\mathcal W$ 和 $\mathcal D$ 分别表示词典和文档库（corpus）。对于每个 $w\in\mathcal W$ , $d\in\mathcal D$ ，我们用 $f(w, d)$ 表示 $w$ 在 $d$ 中出现的次数，用 $L(d)$ 表示 $d$ 中的总词数，用 $w\in d$ 表示 $f(w,d) > 0$ ；同时，我们用 $N(w)$ 来表示词 $w$ 出现的文档数，用 $N$ 表示文档的总数。我们定义

\begin{aligned} \text{tf}(w, d) &= \frac{f(w, d)}{L(d)},\\ \text{idf}(w) &= \log\frac{N}{N(w)}. \end{aligned}

其中 $\text{tf}$ 和 $\text{idf}$ 分别是 term frequency 和 inverse document frequency 的缩写。注意到 $\text{tf}$ 可以衡量一个词在某个文章中出现的频率， $\text{idf}$ 可以衡量某个词的 “稀有程度”，因此 $\text{tf-idf}$ 就是将它们乘起来作为权重。

实践中使用 $\text{tf-idf}$ 的时候还需要考虑一些工程上的问题。由于 $\text{idf}$ 的分母可能为 $0$ ，这会给计算造成麻烦，为了避免这种麻烦，同时也为了让 $\text{idf}$ 在对于频率很小的词的时候表现更加平滑，我们常用修正过的 $\text{idf}$ ，例如像下面这样的式子

\text{idf-smooth} = \log\frac{N + 1}{N(w) + 1} + 1

来进行代替（当然，里面的参数 1 也可以调节成随便什么合理的数值）。关于 $\text{tf}$ ，也可以用类似的策略来平滑化，例如在应用广泛的 BM25 算法中，它考虑了这样的平滑化

\text{tf-smooth} = \frac{f(w, d)(k_1 + 1)}{f(w, d) + k_1(1 - b + b\cdot L(d) / \text{avg}L)},

其中 $k_1, b$ 是参数， $\text{avg}L$ 表示 $L(d)$ 的平均值。总的来说，在实际操作过程中，我们一般用

\sum_{w \in Q}\text{tf-smooth}(w, d)\cdot \text{idf-smooth}(w)

来衡量每个文档 $d$ 与查询 $Q$ 的相关程度。至于 Lucene，它默认采用了一种奇怪的加权

\sum_{w\in Q} \text{tf-smooth}(w, d)^{1/2} \cdot\text{idf-smooth}(w)^2\cdot\text{boost}.

其中 $\text{boost}$ 是用户指定的权重。至于为什么选取这样的指数，我在它的文档中没有看到什么解释。此外，Lucene 为了处理复杂的查询语法，对于不同关键词的权重进行了比较复杂的处理，详情可见这篇文档。

关于更多的相关度计算技术，可以参考 terrier 的文档（预览如下）。

一列算法的清单，包括 BB2, BM25, DFR_BM25, DLH, DLH13 等

当然我们这里考虑的只是朴素的文本查询。对于搜索引擎来说，它还需要衡量不同网页的 “价值”，而这就是一个复杂得多的话题了。

#tf-idf 的信息论解释

我们可以用信息论的角度来简单论证一下 $\text{tf-idf}$ 的合理性（ref：Aizawa, A., 2003. An information-theoretic perspective of tf–idf measures q. Information Processing and Management 21.）。

注意到信息论中的互信息（mutual information）

M(X, Y) = H(X) - H(X \mid Y) = \sum_{x,\ y} p(x, y) \log\frac{p(x, y)}{p(x)p(y)}

这一概念可以用来衡量在知道随机变量 $Y$ 时，变量 $Y$ 的不确定程度减小的程度（其中 $H$ 表示条件熵）。这个减小程度越大，就说明 $X$ 和 $Y$ 的相关性越强。考虑用 $Y$ 看成是一个衡量某个给定关键词在文章中出现情况的随机变量， $X$ 看成是一个随机文档。那么 $M(X, Y)$ 就可以衡量关键词对于这篇文档的重要程度。

$\Omega = \{(w, d) \mid w \in D\}$ 是我们所考虑的概率空间，在这个概率空间中，每个文档被赋予了相同的概率；给定一篇文档 $d$ ， $p(w \mid d)$ 与 $f(w, d)$ 成正比。我们用 $W$ 和 $D$ 表示 $\Omega$ 中代表关键词和文档的随机变量。为了计算 $M(W, D)$ ，我们首先注意到对于每个 $w\in \mathcal W$ , $d\in\mathcal D$ ，若 $w \in d$ ，则

p(d \mid w) = \frac{1}{\# \{d \in \mathcal D : w \in d\}},

反之 $p(d\mid w) = 0$ ，因此我们可以计算出

\begin{aligned} H(D \mid W = w) &= -\sum_{d \in \mathcal D} p(d \mid w)\cdot\log p(d \mid w)\\ &= -\log \frac{1}{\#\{d\in \mathcal D: w \in d\}} \\ &= \log\#\mathcal D - \text{idf}(w) \\ &= H(D) - \text{idf}(w). \end{aligned}

从而

\begin{aligned} M(D, W) &= H(D) - H(D\mid W) = H(D) - \sum_{w\in\mathcal W} p(w) H(D\mid W = w) \\ &= \sum_{w\in\mathcal W} \text{idf}(w)\cdot p(w) \\ &= \sum_{w, d \in \Omega} \text{tf}(w, d) \cdot\text{idf}(w). \end{aligned}

因此我们可以看到， $M(X, Y)$ 即为所有 $\text{tf-idf}$ 的总和。而 $M$ 正是衡量 $D$ 和 $W$ 这两个随机变量的相关程度的，因此 $\text{tf-idf}$ 可以被解释为对于某个特定的文档和关键词，它们对于总的相关程度的贡献值。

#高亮片段

在找到相关的文档之后，为了展示给用户，我们还需要在文档中摘取合适的片段。为了让用户能够一目了然，我们应当使得这个片段中包含相关程度尽可能高的关键词，并且将关键词用醒目的方式标注出来（例如用粗体）。例如在文首的例子中（见下图），这个 wiki 页面里面包含了很多关键词，但是搜索引擎能够向用户展示这样一段相关度很高的片段。

搜索引擎展示了 List of post-punk bands 的 Wiki 条目，其中 post-punk bands, Post-punk 等词被高亮显示出来了

当文档中的关键词比较分散的时候，我们也许需要提供多个片段才能更好地展示信息。

搜索引擎展示了一个 postpunkprof.com 的页面，其中的 1980s, post-punk 等关键词分散地分布在网页中

在文档中找到这样的片段的过程被称为高亮（highlight）。一般来说，高亮的过程还是非常直接的。常见的高亮算法主要分为三个阶段：

将文档（实际上是一堆 token 组成的序列）划分成一些片段（fragment）。
根据一定的算法对于每个片段给一个评分（score）。
挑选出评分最高的一个或几个片段，将它们按照一定顺序（评分高低 / 在文档中的前后顺序）连接起来组成最后高亮文本。

这些部分的实现就是比较工程化的问题了。对于 swoosh，它默认的 ContextFragmenter 的实现方式是在每一个查询词的附近找一块 “大小适中” 的区域。对于第二个部分，swoosh 的实现如下：

# Add up the boosts for the matched terms in this passage
score = sum(t.boost for t in f.matches)  # boost 表示权重

# Favor diversity: multiply score by the number of separate
# terms matched
score *= (len(f.matched_terms) * 100) or 1

return score

可以看到 swoosh 的实现是比较粗糙的。Lucene 的 Unified Highlighter 则提供了更精确（虽然可能更慢）的实现方法：先将文档按照标点符号切割成句子，然后将文档视为一个 corpus，把每个句子视为一个 document，使用 BM25 对每个句子进行评分。

#More about

有了上面这些功能，一个能用的全文检索工具就可以搭建起来了。不过，如果想要做到 “更好的用户体验” 的话，还有一些其它的功能可供实现。这里提供一例（以后有空再加）：

#拼写纠错

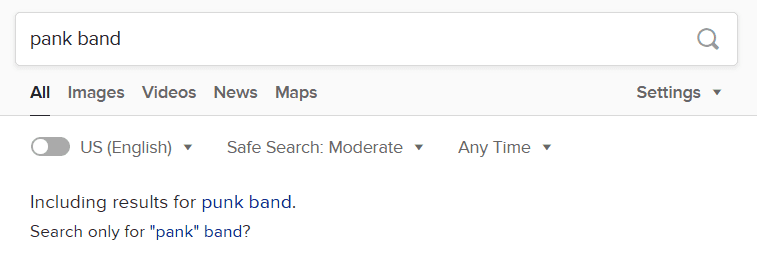
拼写纠错。例如当我搜索 “pank band” 的时候，duckduckgo 就会提示 Including results for "punk band"? ，如下图所示。

当搜索 pank band 时，搜索引擎会提示「你是否要找的是 punk band」

在讨论这个功能是如何实现之前，我们需要一些预备知识：Levenshtein distance 是一个衡量两个字符串的距离的方式，如果一个字符串需要最少 k 次修改才能变成另一个，那么它们的 Levenshtein distance 即为 k。有一种高效的算法，即 Levenshtein automaton 可以生成和识别与某个字符串之间的 Levenshtein distance 距离不大于 k 的所有字符串。有研究指出大部分的 typo 所造成的 Levenshtein distance 都不大于 2（ Ref: F. J. Damerau. A technique for computer detection and correction of spelling errors. Communications of the ACM, 7(3):171–176, 1964.）。

对于这个功能，swoosh 提供了两个实现。对于第一个实现，swoosh 就是通过 Levenshtein automaton，遍历所有与关键词的 Levenshtein distance 小于某个阈值的词，查询它们在单词表中是否存在，如果存在则给出纠错提示（非常暴力）。对于第二个实现，swoosh 则是通过在索引中寻找与关键词的 Levenshtein distance 小于某个阈值的词，根据这个词的频率与实际的 Levenshtein distance 给出一个 score，然后将这些建议词按照 score 排序，给出 score 最高的建议词。

当然 swoosh 的实现是很粗糙的，它只能提供单个单词的纠错，无法考虑上下文的联系（例如在 duckduckgo 里面搜索 pank 这单个单词的时候，它并不会提醒我修改成 punk）。实际应用中会使用更复杂的方法，例如使用 n-gram 的频率而不是使用单个单词的频率来进行 scoring。

#Post Script

虽然本文花了这样的篇幅讲了如何实现一个全文检索引擎，不过很羞愧，自己并没有手动实现一个。毕竟 whoosh 已经足够好用了，特别是对于像我这样的轻度需求来说。如果需要动手实现的话，序列化协议的设计是一个比较麻烦的问题（除非完全不在乎效率），这个模块一般被称为 codec，一般很少有人去碰这一块。调优读写索引的过程是实现高效的全文检索引擎的一个比较关键的部分，这一方面可以找到许多相关的文章，因此本文中没有对此进行复述。